前人遇到的问题：RNN需要按照时间顺序地完成每个步骤无法并行训练，ViT受到注意力计算二次复杂性的限制。

提示

本部分内容部分参考自：CSDN：一文通透想颠覆Transformer的Mamba：从SSM、HiPPO、S4到Mamba

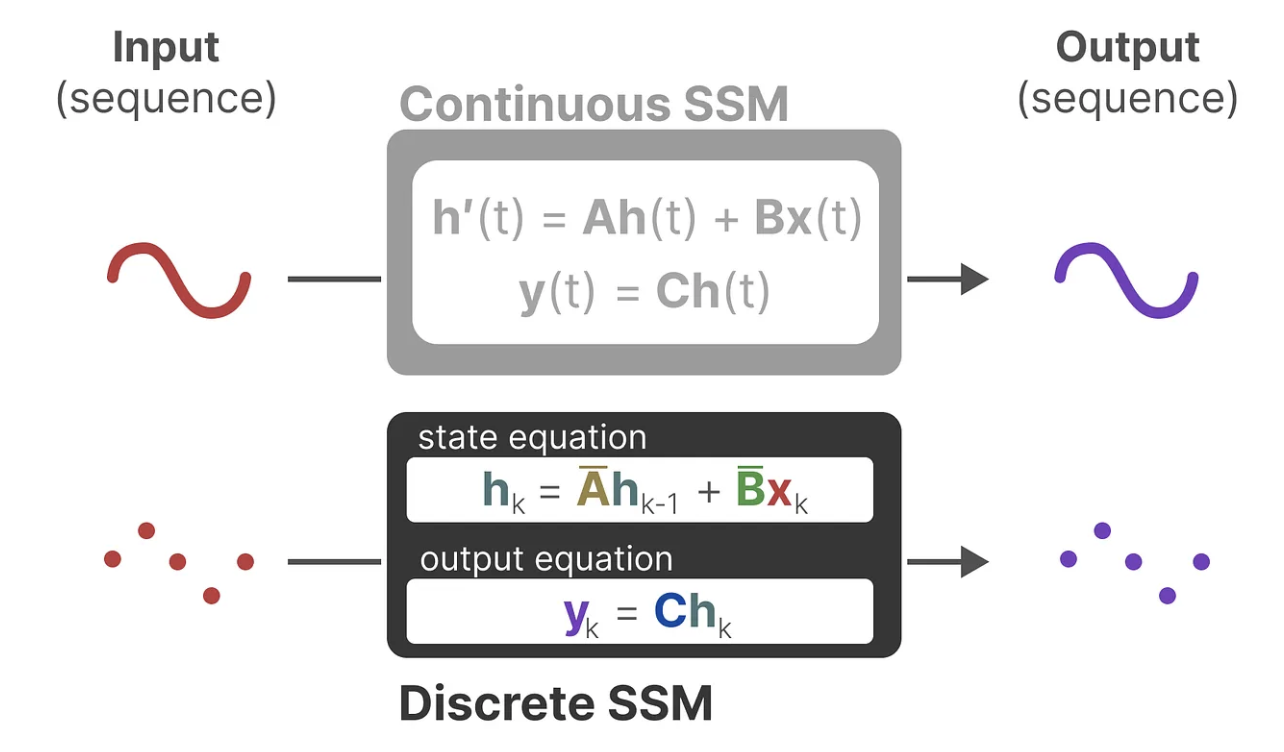
SSM

状态空间模型SSM：RNN本质就是一个SSM，SSM 是用于描述这些状态表示并根据某些输入预测其下一个状态可能是什么的模型。一般SSMs包括映射输入序列x(t)、潜在状态表示h(t)、预测输出序列y(t)。

$$\mathbf{h^{\prime}(t)=Ah(t)+Bx(t)}$$

$$\mathbf{y}(\mathbf{t})=\mathbf{Ch}(\mathbf{t})+\mathbf{Dx}(\mathbf{t})$$

上面的第一个方程是不和RNN循环结构：$h_{t}=tanh \left(W h_{t-1}+U x_{t}\right)$ 非常类似：通过上一个隐藏状态和当前输入综合得到当前的隐藏状态，只是两个权重W、U换成了A、B两个系数，且去掉了非线性的激活函数tanh。

但系数A代表着什么，其实A就是存储着之前所有历史信息的浓缩精华(可以通过一系列系数组成的矩阵表示之)，以基于A更新下一个时刻的空间状态hidden state。

总之，通过求解这些方程，可以根据观察到的数据：输入序列和先前状态，去预测系统的未来状态。SSM的关键是找到：状态表示(state representation)——$h(t)$，以便结合「其与输入序列」预测输出序列。

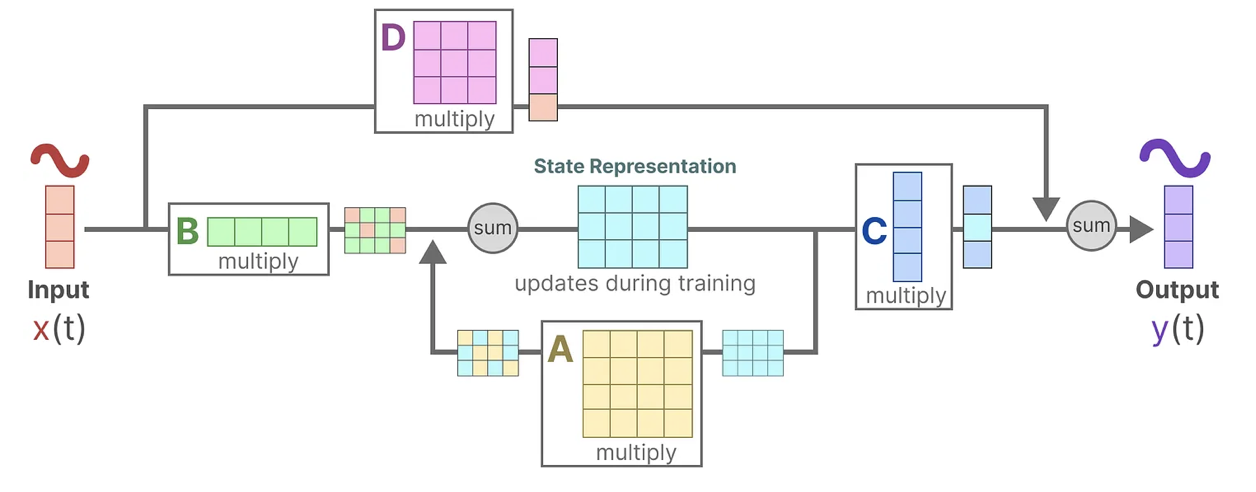
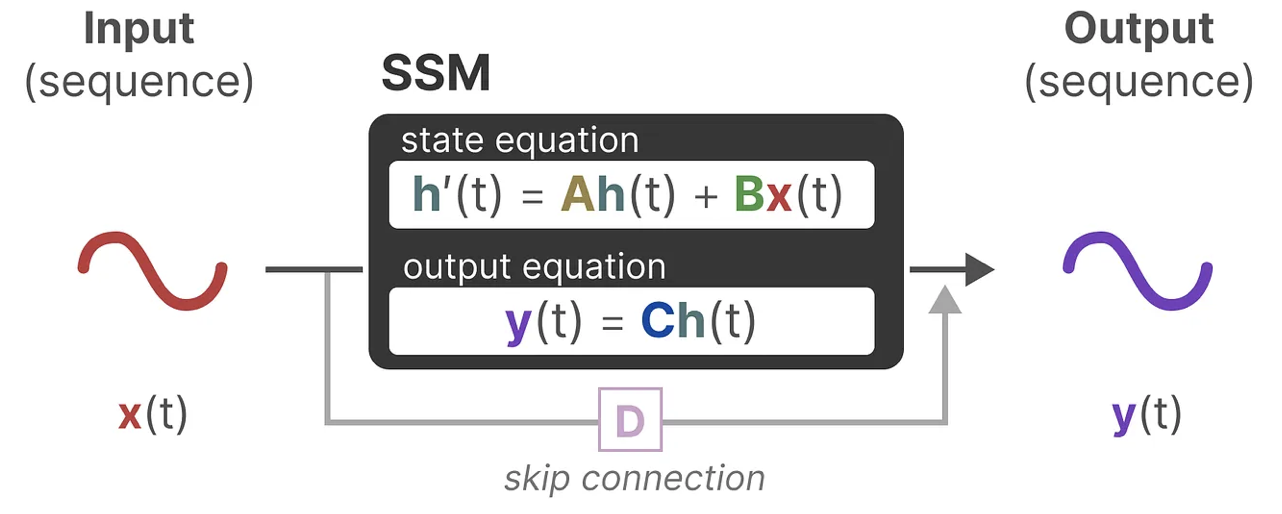
总之，这两个方程共同旨在根据观测数据预测系统的状态，且考虑到输入一般都是连续的，因此SSM的主要表示是连续时间表示( continuous-time representation )

提示

以上这些东西，是1960年在ASME会议上提出的State Space Machine! SSM由Kalman提出，原论文：A New Approach to Linear Filtering and Prediction Problems

SSM to S4

离散化SSM

由于除了连续的输入之外，还会通常碰到离散的输入(如文本序列)，不过，就算SSM在离散数据上训练，它仍能学习到底层蕴含的连续信息，因为在SSM眼里，sequence不过是连续信号signal的采样，或者说连续的信号模型是离散的序列模型的概括。那模型如何处理离散化数据呢？答案是可以利用零阶保持技术(Zero-order hold technique)。

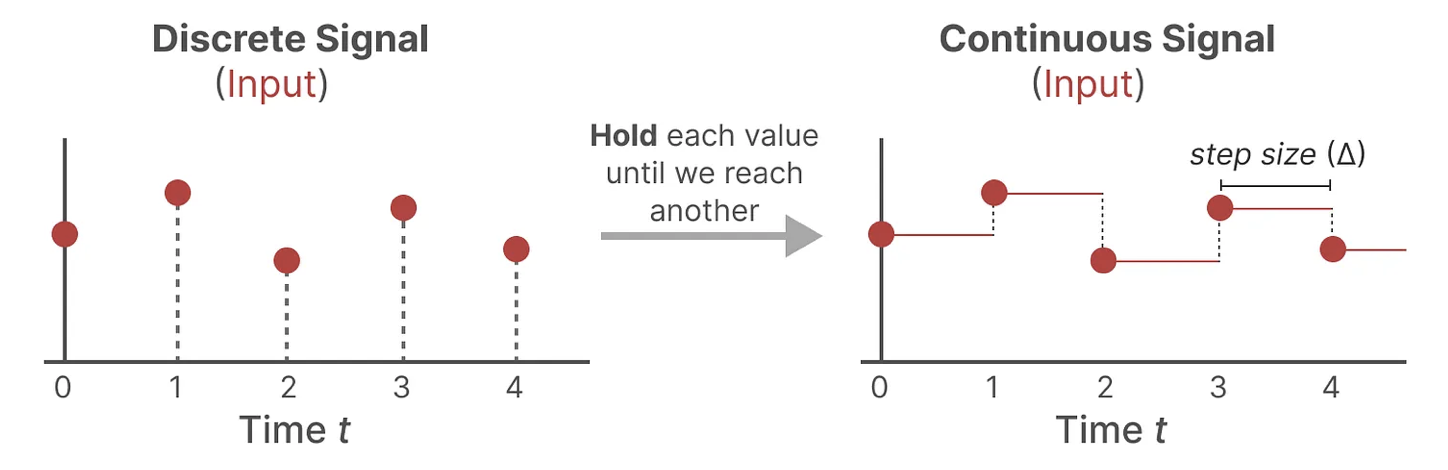
当输入连续后，我们可以生成一个连续的输出，并且只根据输入的时间步长对值进行采样。这个采样的值就是我们离散化的输出。

离散化方法有几种比较有效，如欧拉方法、零阶保持器(Zero-order Hold, ZOH)方法或双线性方法。欧拉方法是最弱的，但在后两种方法之间的选择是微妙的。事实上，S4论文采用的是双线性方法，但Mamba使用的是ZOH。

提示

这里说的离散化，并不是连续数据离散化方法（包括等距离散法、等频率离散法、K-means模型离散法、分位数离散法、二值化离散法、基于卡方分裂的离散法等），而是自动控制原理里的连续系统离散化。具体可以参考：一文书尽离散化——连续系统离散化原理及应用。

那么状态空间方程应该如何离散化呢？SSM给出的答案是：

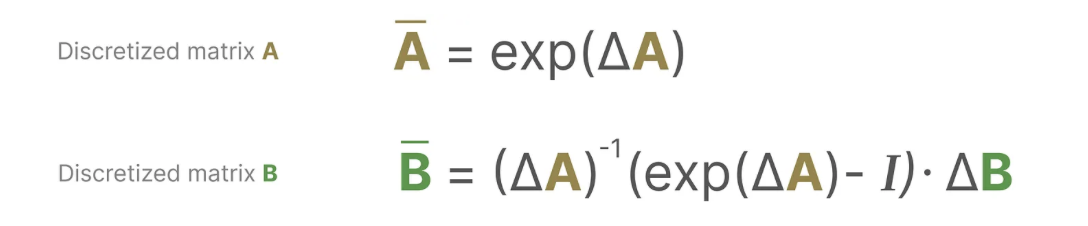
那么为什么在离散化的过程中，AB矩阵是这样变化的呢？这其实也是现代控制理论中的状态空间方程离散化的内容，具体可以参照：状态空间方程的离散化，文中有关于这两个矩阵如何得来的数学推导。

注意：我们在保存时，仍然保存矩阵A的连续形式(而非离散化版本)，只是在训练过程中，连续表示被离散化(During training, the continuous representation is discretized)。

循环/卷积表示

循环结构表示以快速推理

离散 SSM 允许可以用离散时间步长重新表述问题，在每个时间步，都会涉及到隐藏状态的更新（比如$h_k$取决于$\overline{\mathbf{B}} \mathbf{x}_{\mathrm{k}}$和$\overline{\mathbf{A}} \mathbf{h}_{\mathrm{k}-1}$的共同作用结果，然后通过$Ch_k$预测输出$y_k$）。

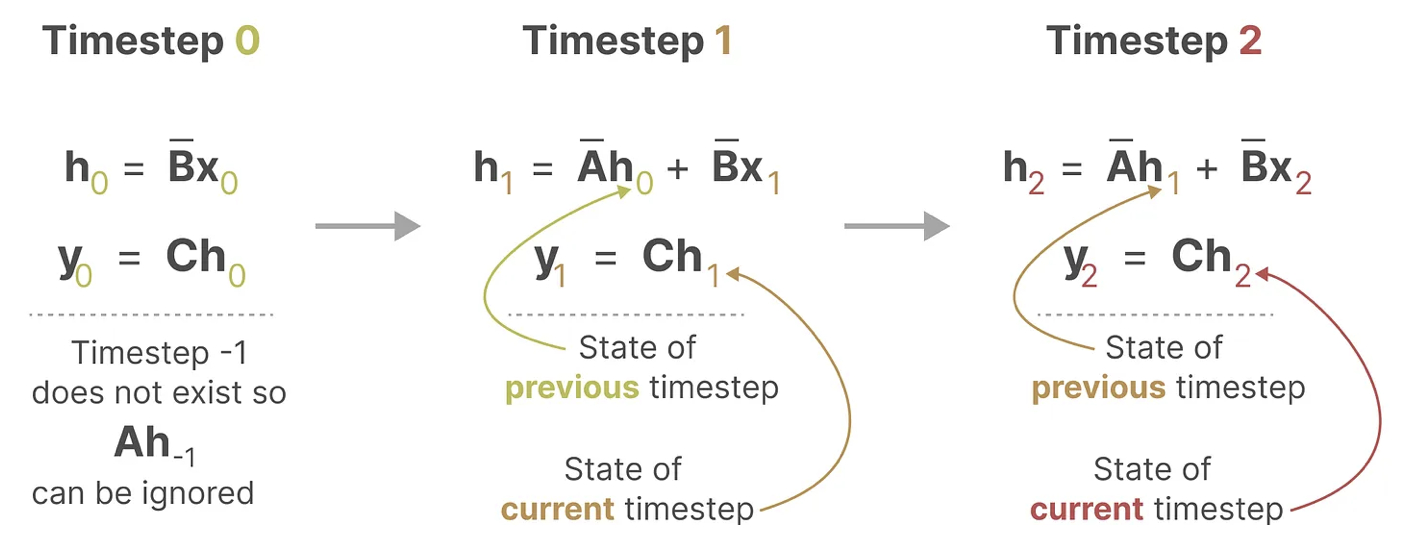
有没有发现这就和RNN的方式一样了？如此就可以用RNN的结构来处理。

这时，我们再把y的公式推导一下后面会用到：

$$\begin{aligned} y_{2} &=Ch_{2}=C\left(\bar{A}h_{1}\bar{B}x_{2}\right) \\ &=C\left(\bar{A}\left(\bar{A}h_0\bar{B}x_1\right)\bar{B}x_2\right) \\ &=C\left(\bar{A}\left(\bar{A}\cdot\bar{B}x_0\bar{B}x_1\right)\bar{B}x_2\right) \\ &=C\begin{pmatrix}\bar{A}\cdot\bar{A}\cdot\bar{B}x_{0}\bar{A}\cdot\bar{B}x_{1}\bar{B}x_{2}\end{pmatrix} \\ &=C\cdot\bar{A}^{2}\cdot\bar{B}x_{0}C\cdot\bar{A}\cdot\bar{B}\cdot x_{1}C\cdot\bar{B}x_{2} \end{aligned}$$

卷积结构表示以并行训练

在经典的图像识别任务中，我们用过滤器(即卷积核kernels)来导出聚合特征，而SSM也可以表示成卷积的形式：

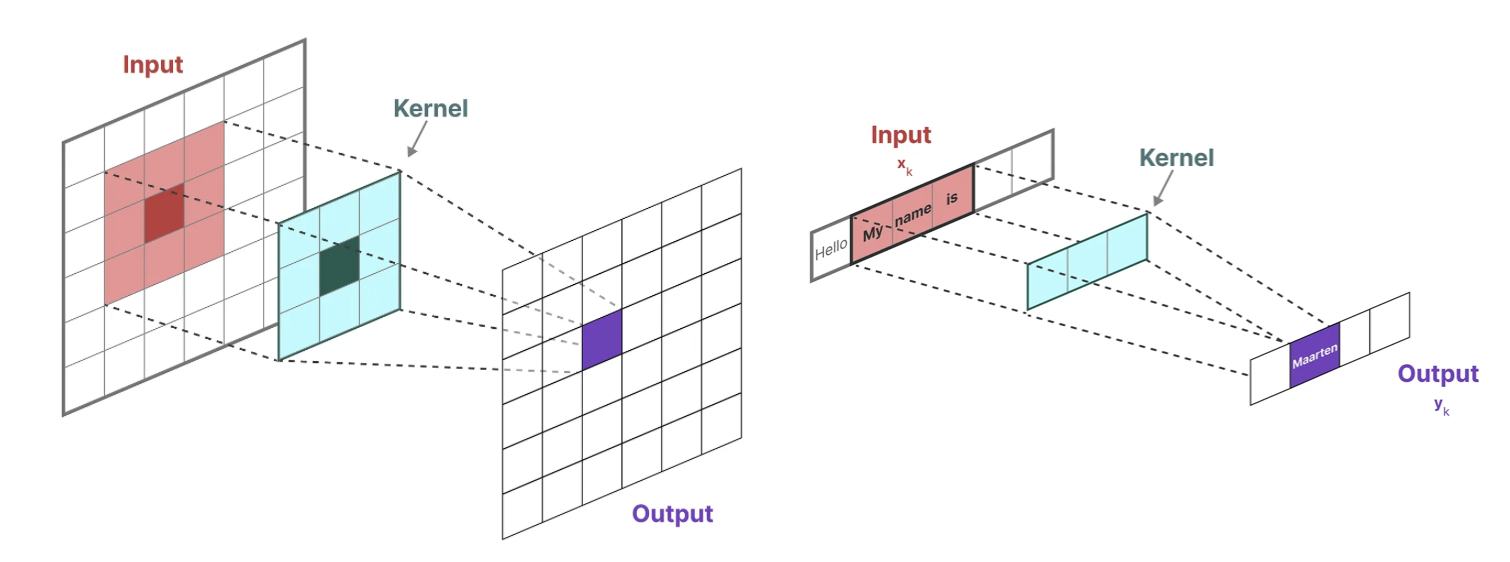
而用来表示这个“过滤器”的内核源自 SSM 公式:

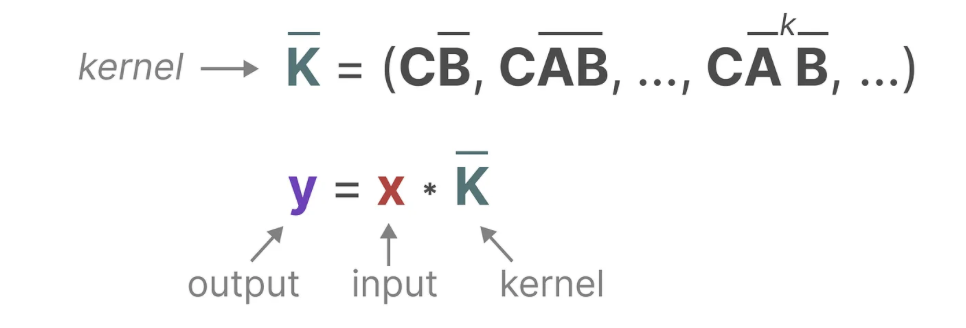
怎么理解这个公式呢？举个例子：

1. 与卷积一样，我们可以使用 SSM 内核来检查每组token并计算输出
2. 内核将移动一次以执行下一步的计算
3. 最后一步，我们可以看到内核的完整效果：

至于上图中的是咋计算得到的，别忘了上面推导出来的：

$$\begin{aligned} y_{2} &=Ch_{2}=C\left(\bar{A}h_{1}\bar{B}x_{2}\right) \\ &=C\left(\bar{A}\left(\bar{A}h_0\bar{B}x_1\right)\bar{B}x_2\right) \\ &=C\left(\bar{A}\left(\bar{A}\cdot\bar{B}x_0\bar{B}x_1\right)\bar{B}x_2\right) \\ &=C\begin{pmatrix}\bar{A}\cdot\bar{A}\cdot\bar{B}x_{0}\bar{A}\cdot\bar{B}x_{1}\bar{B}x_{2}\end{pmatrix} \\ &=C\cdot\bar{A}^{2}\cdot\bar{B}x_{0}C\cdot\bar{A}\cdot\bar{B}\cdot x_{1}C\cdot\bar{B}x_{2} \end{aligned}$$

以此内推，可得:

$$y_{3}=\mathbf{C} \overline{\mathbf{A}} \overline{\mathbf{A}} \overline{\mathbf{A}} \overline{\mathbf{B}} x_{0}+\mathbf{C} \overline{\mathbf{A}} \overline{\mathbf{A}} \overline{\mathbf{B}} x_{1}+\mathbf{C} \overline{\mathbf{A}} \overline{\mathbf{B}} x_{2}+\mathbf{C} \overline{\mathbf{B}} x_{3}$$

换个形式看，是不意味着$y_3$实际上可以计算为点积，其中右侧向量是我们的输入$x$:

$$y_{3}=\left(\begin{array}{llll} \mathbf{C} \overline{\mathbf{A}} \overline{\mathbf{A}} \overline{\mathbf{A}} \overline{\mathbf{B}} & \mathbf{C} \overline{\mathbf{A}} \overline{\mathbf{A}} \overline{\mathbf{B}} & \mathbf{C} \overline{\mathbf{A}} \overline{\mathbf{B}} & \mathbf{C} \overline{\mathbf{B}} \end{array}\right)\left(\begin{array}{l} x_{0} \\ x_{1} \\ x_{2} \\ x_{3} \end{array}\right)$$

由于其中三个离散参数A、B、C都是常数，因此我们可以预先计算左侧向量并将其保存为卷积核，这为我们提供了一种使用卷积超高速计算y的简单方法，如以下两个方程所示:

$$\begin{aligned} \overline{\mathbf{K}} & =\left(\begin{array}{llll} \mathbf{C} \overline{\mathbf{B}} & \mathbf{C} \overline{\mathbf{A}} \overline{\mathbf{B}} & \cdots & \mathbf{C A}^{\mathbf{k}} \overline{\mathbf{B}} \end{array}\right) \\ y & =\overline{\mathbf{K}} * x \end{aligned}$$

至此，总结一下，将 SSM 表示为卷积的一个主要好处是它可以像卷积神经网络CNN一样进行并行训练。然而，由于内核大小固定，它们的推理不如 RNN 那样快速。

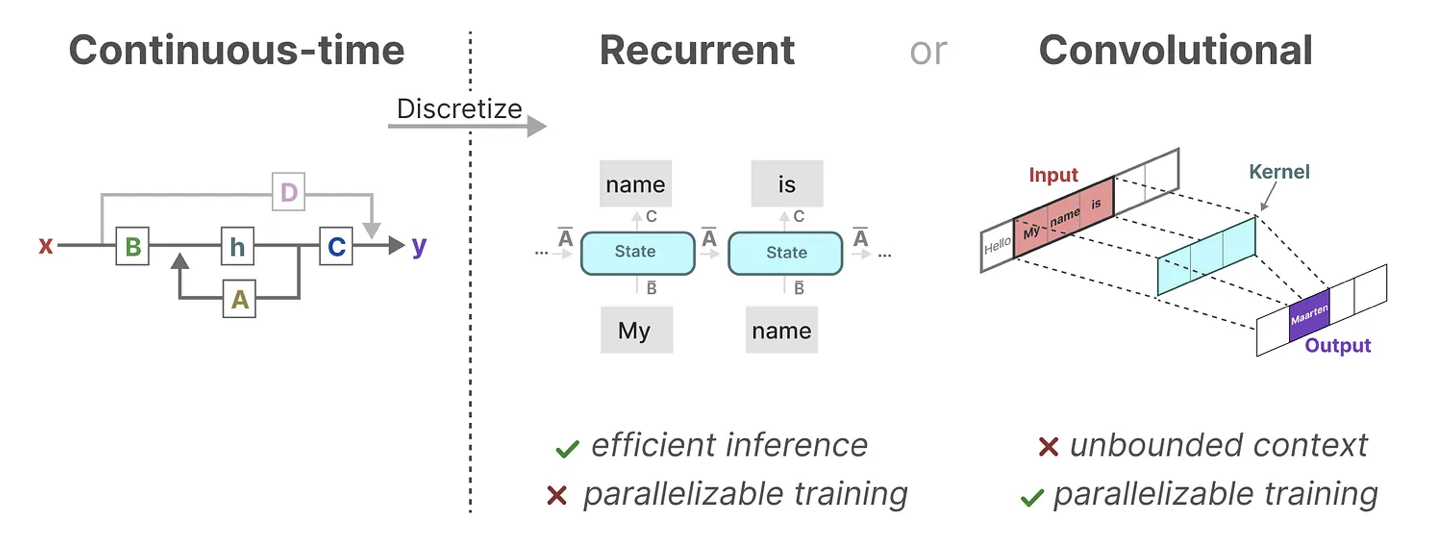
那有没两全其美的办法呢？最终是有的：

1. 作为从输入信号到输出信号的参数化映射，SSMs可以当做是RNN与CNN的结合「These models can be interpreted as acombination of recurrent neural networks (RNNs) and convolutional neural networks (CNNs)」，即推理用RNN结构，训练用CNN结构，这就是Mamba最无敌的地方。

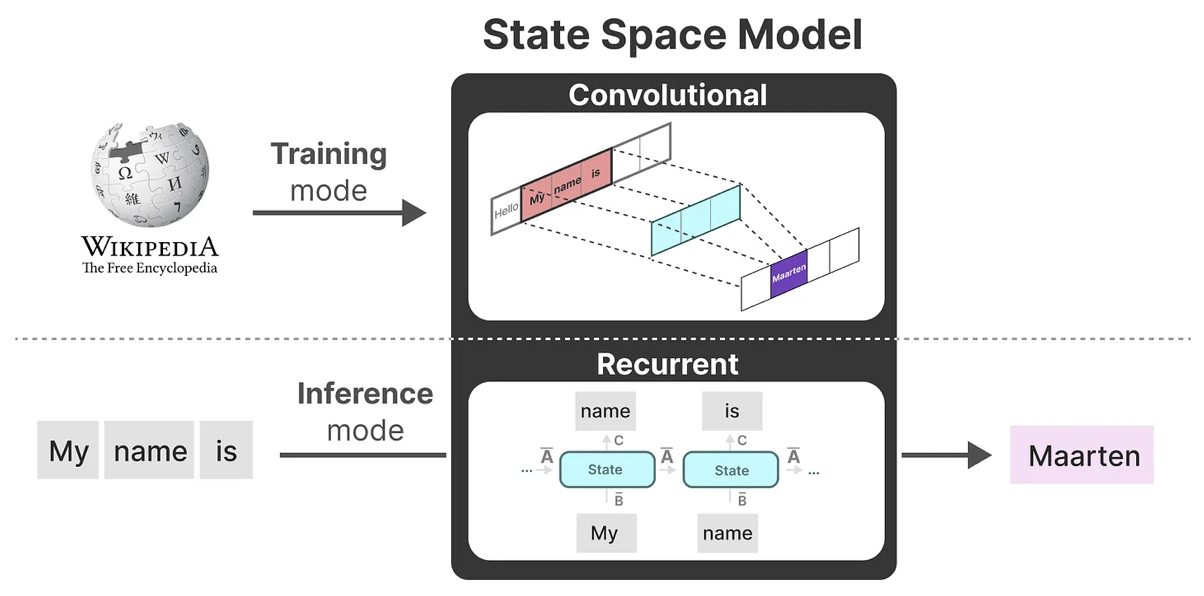
2. 总之，这类模型可以非常高效地计算为递归或卷积，在序列长度上具有线性或近线性缩放(This class of models can be computed very efficiently as either arecurrence or convolution, with linear or near-linear scaling in sequence length)。

基于HiPPO处理长序列

如我们之前在循环表示中看到的那样，矩阵A捕获先前previous状态的信息来构建新状态$(h_k = \overline{A} h_{k-1} + \overline{B} x_k$，当$k = 5$时，则有$h_5 = \overline{A} h_{4} + \overline{B} x_5)$。其实，某种意义上，算是矩阵A产生了隐藏状态(matrix A produces the hidden state)。由于矩阵A只记住之前的几个token和捕获迄今为止看到的每个token之间的区别，特别是在循环表示的上下文中，因为它只回顾以前的状态（因为它只和$h_{t-1}$相乘）。

那么我们怎样才能以保留比较长的memory的方式创建矩阵A呢？

• 答案是可以使用Hippo(Hippo的全称是High-order Polynomial Projection Operator)，解决如何在有限的存储空间中有效地解决序列建模的长距离依赖问题。

• HiPPO尝试将当前看到的所有输入信号压缩为系数向量(HiPPO attempts to compress all input signals it has seen thus far into a vector of coefficients)。

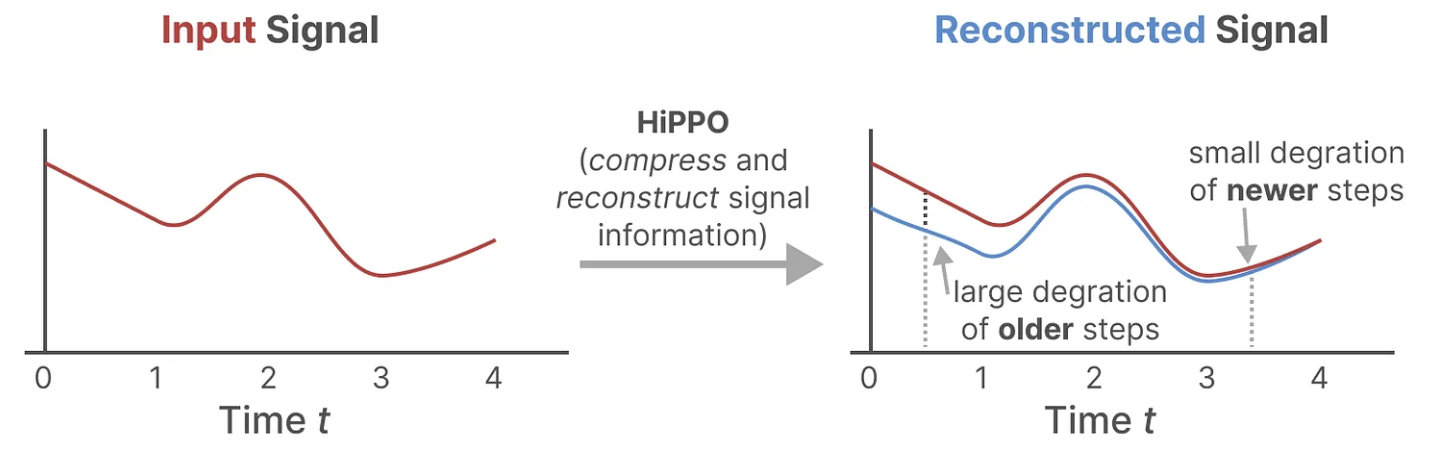
它使用矩阵构建一个“可以很好地捕获最近的token并衰减旧的token”状态表示(to build a state representation that captures recent tokens well and decays older tokens)，说白了， 通过函数逼近产生状态矩阵 A 的最优解，其公式可以表示如下:

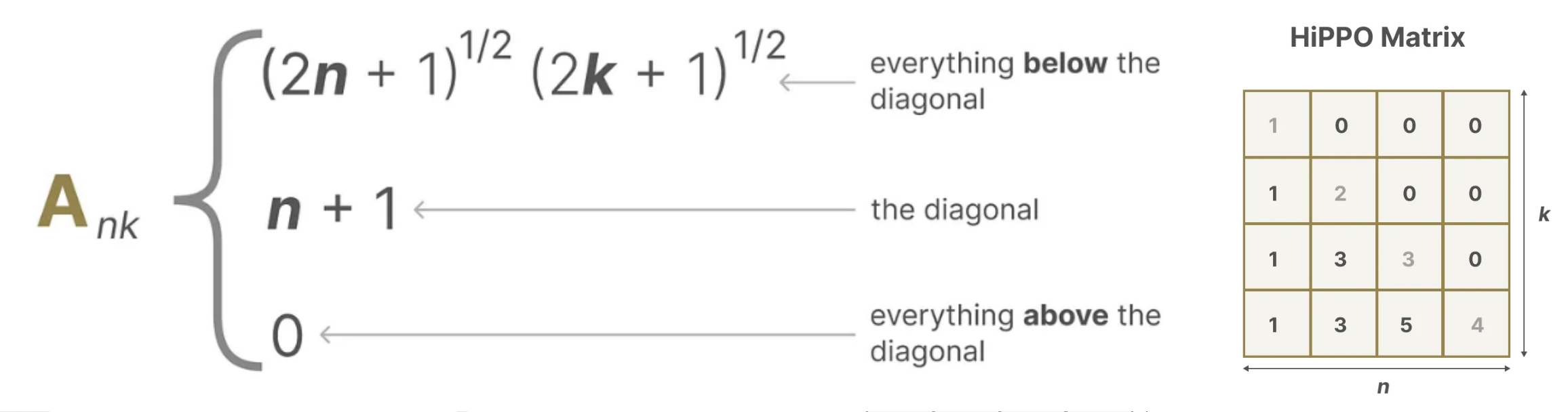
正由于HiPPO 矩阵可以产生一个隐藏状态来记住其历史（从数学上讲，它是通过跟踪Legendre polynomial的系数来实现的，这使得它能够逼近所有以前的历史），使得在被应用于循环表示和卷积表示中时，可以处理远程依赖性。

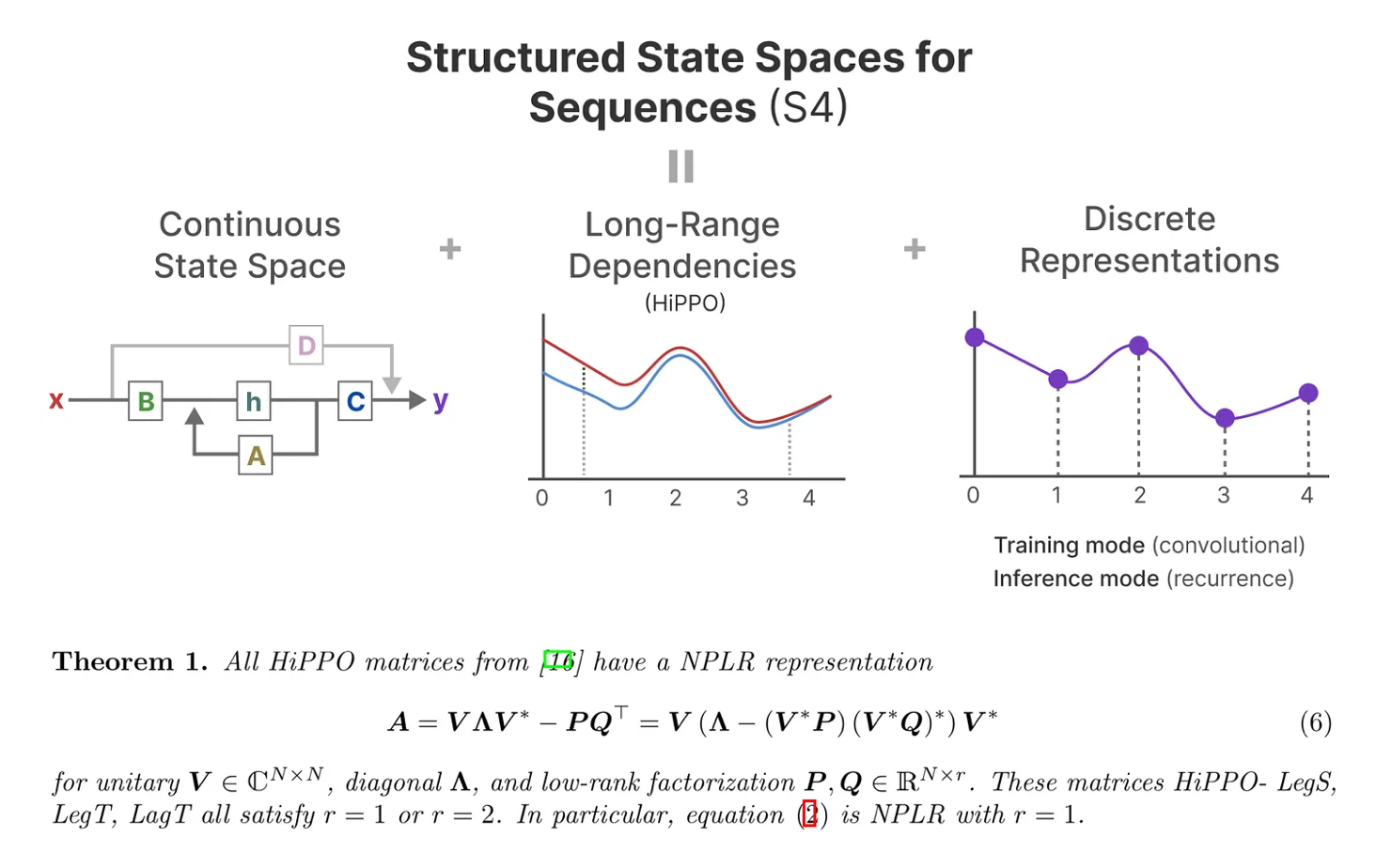
如此，S4的定义就出来了：序列的结构化状态空间——Structured State Space for Sequences，一类可以有效处理长序列的 SSM。

Mamba

mamba(其对应论文为：Mamba: Linear-Time Sequence Modeling with Selective State Spaces)，在语言、音频、DNA序列模态上都实现SOTA，在最受关注的语言任务上，Mamba-3B超越同等规模的Transformer，与两倍大的Transformer匹敌，并且相关代码、预训练模型checkpoint都已开源

简言之，Mamba是一种状态空间模型(SSM)，建立在更现代的适用于深度学习的结构化SSM (简称S6)基础上，与经典架构RNN有相似之处。

Mamba的三大创新

Mamba = 有选择处理信息 + 硬件感知算法 + 更简单的SSM架构

• 对输入信息有选择性处理(Selection Mechanism)
• 硬件感知的算法(Hardware-aware Algorithm)

该算法采用“并行扫描算法”而非“卷积”来进行模型的循环计算(使得不用CNN也能并行训练)，但为了减少GPU内存层次结构中不同级别之间的IO访问，它没有具体化扩展状态。
当然，这点也是受到了S5(Simplified State Space Layers for Sequence Modeling)的启发。

• 更简单的架构

将SSM架构的设计与transformer的MLP块合并为一个块(combining the design of prior SSM architectures with the MLP block of Transformers into a single block)，来简化过去的深度序列模型架构，从而得到一个包含selective state space的架构设计

选择性状态空间模型：从S4到S6

作者认为，序列建模的一个基础问题是把上下文压缩成更小的状态(We argue that a fundamental problem of sequence modeling is compressing context into a smaller state)，从这个角度来看：

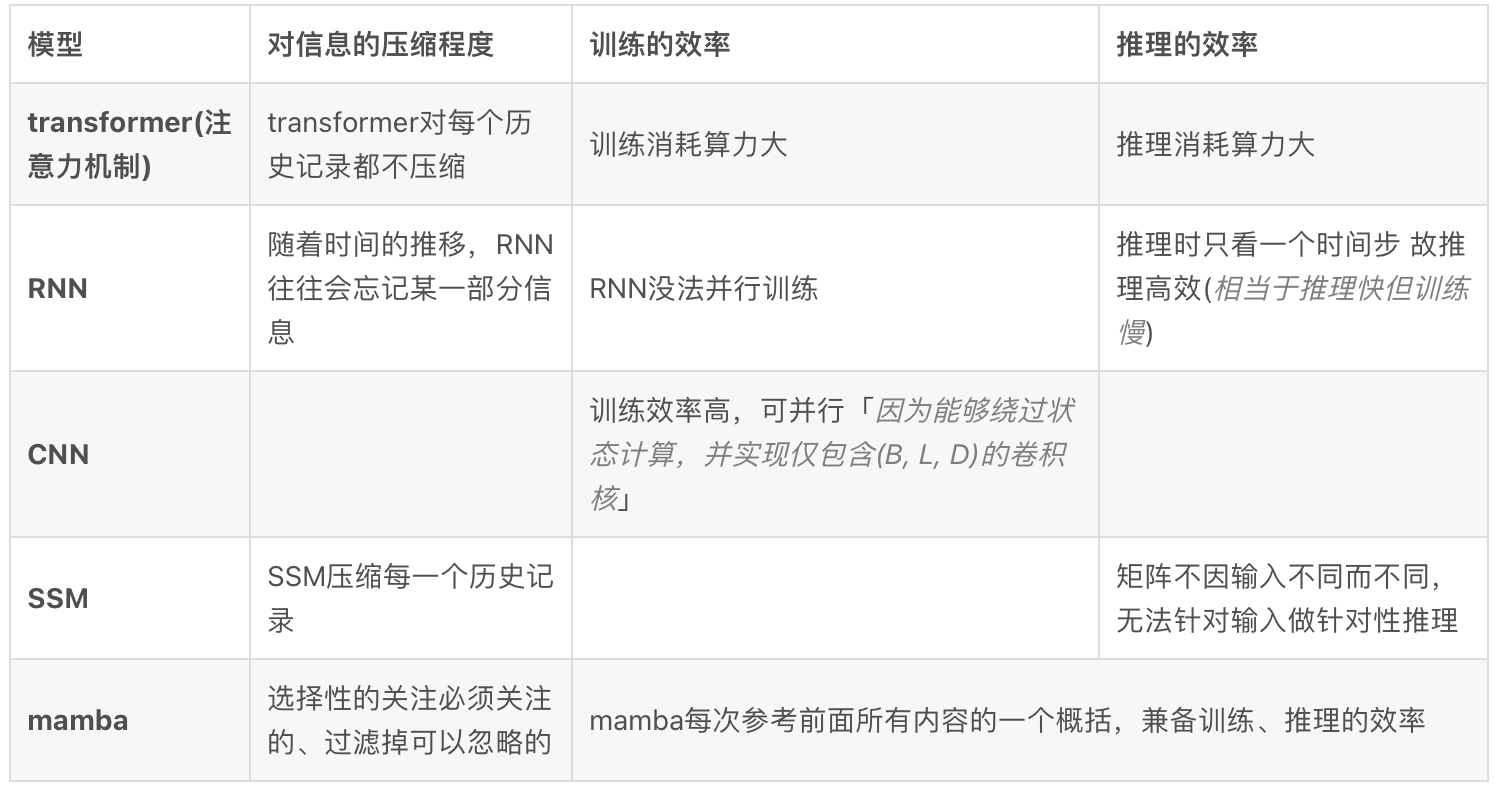
• transformer的注意力机制虽然有效果但效率不算很高，毕竟其需要显式地存储整个上下文(storing the entire context，也就是KV缓存)，直接导致训练和推理消耗算力大 好比，Transformer就像人类每写一个字之前，都把前面的所有字+输入都复习一遍，所以写的慢

• RNN的推理和训练效率高，但性能容易受到对上下文压缩程度的限制：On the other hand, recurrent models are efficient because they have a finite state, implying constant-time inference and linear-time training. However, their effectiveness is limited by how well this state has compressed the context.

  好比，RNN每次只参考前面固定的字数(仔细体会这句话：When generating the output, the RNN only needs to consider the previous hidden state and current input. It prevents recalculating all previous hidden states which is what a Transformer would do)，写的快是快，但容易忘掉更前面的内容

• 而SSM的问题在于其中的矩阵A B C不随输入不同而不同，即无法针对不同的输入针对性的推理。

最终，Mamba的解决办法是，相比SSM压缩所有历史记录，mamba设计了一个简单的选择机制，通过“参数化SSM的输入”，让模型对信息有选择性处理，以便关注或忽略特定的输入. 这样一来，模型能够过滤掉与问题无关的信息，并且可以长期记住与问题相关的信息. 好比，Mamba每次参考前面所有内容的一个概括，越往后写对前面内容概括得越狠，丢掉细节、保留大意.

mamba前身S4的4个参数的不随输入不同而不同

首先，在其前身S4中，其有4个参数($\Delta, A, B, C$)，且它们不随输入变化(即与输入无关)，这些参数控制了以下两个阶段：

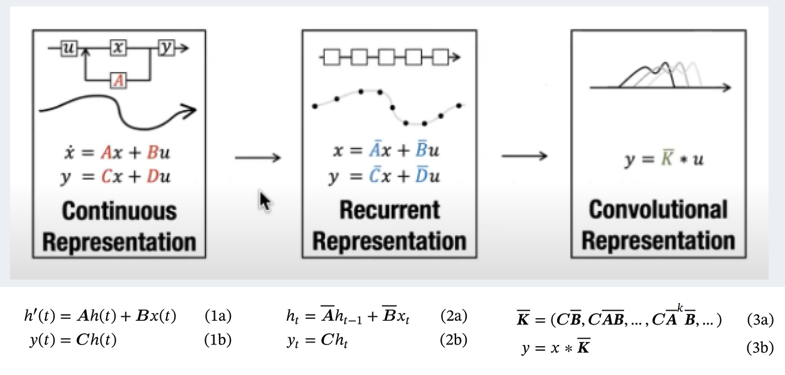
从图中可以看到，模型可以用两种方式计算，即线性递归(2)或全局卷积(3)，模型通常使用卷积模式(3)可以进行高效的并行化训练，并切换到循环模式(2)以高效的自回归推理(其中输入每次只看到一个时间步)。

S4中三个矩阵的维度表示、维度变化

再回顾一下，通过之前的讲解，可知$A ∈ ℝ_{𝑁×𝑁}, B ∈ ℝ_{𝑁×1} , C ∈ ℝ_{1×𝑁}$矩阵都可以由$N$这个数字表示（the $A ∈ ℝ_{𝑁×𝑁}, B ∈ ℝ_{𝑁×1} , C ∈ ℝ_{1×𝑁}$ matrices can all be represented by 𝑁 numbers.）

但为了对批量大小为B(Batch size)、L(length)、D(Dimension)的输入序列，Mamba的处理方式是对这D个dimension的每个dimension都搞一个独立的SSM，即SSM被独立的应用于每个通道。这就解释了为什么下图中的A、B、C三个矩阵的第一个维度是都是 D：

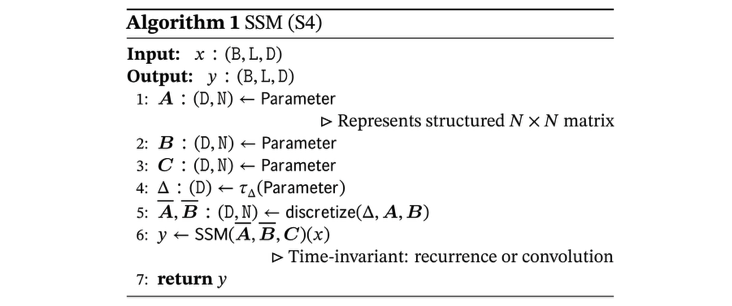
提示

这里是不是有可以优化的地方？通道间应该有信息交换，或者给SSM加一个模块用于通道间信息交换是不是会效果更好些？

mamba：从S4到S6的算法变化流程

最后，在Mamaba中，作者让B矩阵、C矩阵、$\Delta$成为输入的函数，让模型能够根据输入内容自适应地调整其行为：

• 从S4到S6的过程中，影响输入的B矩阵、影响状态的C矩阵的大小从原来的(D,N)变成了(B,L,N)。
• 且$\Delta$的大小由原来的D变成了(B,L,D)，意味着对于一个 batch 里的 每个 token (总共有 BxL 个)都有一个独特的$\Delta$
• 且每个位置的B矩阵、C矩阵、$\Delta$都不相同，这意味着对于每个输入token，现在都有独特不同的B矩阵、C矩阵，可以解决内容感知问题。

维度上的变化具体执行时是怎么实现的呢？好办，通过

$$sB(x)=LinearN(x) \\ sC(x)=LinearN(x) \\ sΔ(x)=LinearD(x) \\ τΔ= softplus$$

来逐一将B,C,Δ变成输入数据依赖化(data dependent)。其中对于矩阵B、C的 $Linear_N(x)$代表把维的输入向量x经过一个线性层映射到维，有点类似从之前的$64 × 3(N × D)$变成$10000 × 64(L × N)$，不过，读到此处的你，可曾想为何不是变成$10000 × 64 × 3(L × N × D)$呢？ 一个可能的原因是$\bar{B}=(\Delta A)^{-1}(\exp(\Delta A)-I)\cdot\Delta B$，而和都有这个维度，也就是说$\bar{B}$最终也会具备这个维度。

虽然没有变成data dependent，但是通过SSM的离散化操作之后，($\bar{A},\bar{B}$)会经过outer product变成(B, L, N, D)的data dependent张量，算是以一种parameter efficient的方式来达到data dependent的目的 且换个角度看，离散化之后$\bar{A}=exp(ΔA)$， 的“输入数据依赖性”能够让整体的$\bar{A}$与输入相关。

当然，到底效果变好的最大原因是哪一块，可以参考这篇做下相关的实验：Gated Linear Attention Transformers with Hardware-Efficient Training。

接下来，关键来了，我们再仔细研究下各个变量的含义及其与所谓门控之间的联系(顺带帮你一针见血的指出如果各个变量变成可变的，会发生什么):

$\Delta$类似遗忘门:

较小的步长Δ会忽略特定单词，而更多地使用先前的上文，而较大的步长Δ会更多地关注输入单词而不是上文。如果某个输入比较重要，它的步长就更长些，被重点关注。如果某个输入不太重要 它的步长就短，被直接忽略。从而对于不同的输入，达到选择性关注或忽略的目标，做到详略得当，主次分明。

B起到的作用类似于：进RNN的memory；C起到的作用类似于：取RNN的memory。

如果修改B和C可以允许模型更精细地控制是否让输入x进入状态 h，或状态h进入输出 y，所以 B 和 C 类似于 RNN 中的输入门和输出门。所以有人说，data dependent的B/C的功能跟RNN的input/output gate类似。

A，意味着对应这个维度的SSM来说，A在每个hidden state维度上的作用可以不相同，起到multi-scale/fine-grained gating的作用，这也是LSTM网络里面用element-wise product的原因。

总之，Mamba通过合并输入的序列长度和批量大小来使矩阵B和C，甚至步长Δ取决于输入(其意味着对于每个输入token，现在有不同的B和C矩阵，可以解决内容感知问题)，从而达到选择性地选择将哪些内容保留在隐藏状态以及忽略哪些内容的目标。

硬件感知的设计

硬件感知的设计：并行扫描(parallel scan)且借鉴Flash Attention。

如之前所述，由于A B C这些矩阵现在是动态的了，因此无法使用卷积表示来计算它们(CNN需要固定的内核)，因此，我们只能使用循环表示，如此也就而失去了卷积提供的并行训练能力。

so，为了实现并行化，让我们探讨如何使用循环计算输出。

每个状态比如$H_1$都是前一个状态比如$H_0$乘以$\bar{A}$，加上当前输入$X_1$乘以$\bar{B}$的总和，这就叫扫描操作(scan operation)，可以使用 for 循环轻松计算，然而这种状态之下想并行化是不可能的(因为只有在获取到前一个状态的情况下才能计算当前的每个状态)。

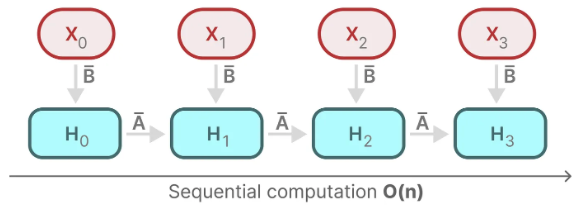
好在mamba通过并行扫描(parallel scan)算法使得最终并行化成为可能，其假设我们执行操作的顺序与关联属性无关，因此，我们可以分段计算序列并迭代地组合它们，即动态矩阵B和C以及并行扫描算法一起创建选择性扫描算法(selective scan algorithm)：

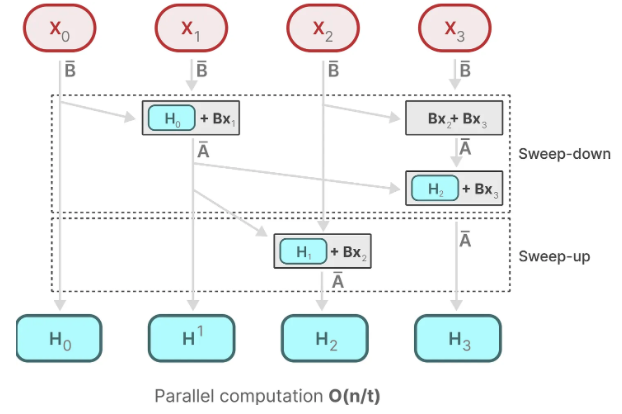
提示

这里好像还是没有说明白并行扫描……

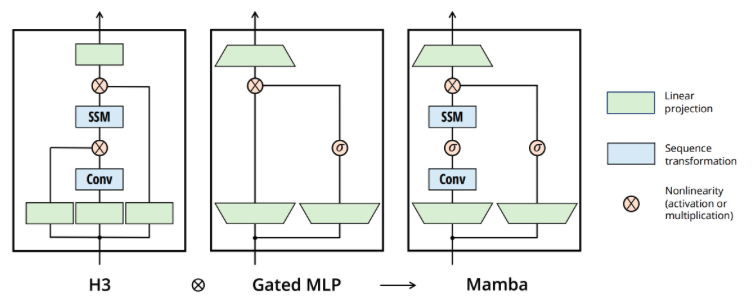
简化的SSM架构

将大多数SSM架构比如H3的基础块，与现代神经网络比如transformer中普遍存在的门控MLP相结合，组成新的Mamba块，重复这个块，与归一化和残差连接结合，便构成了Mamba架构：

Mamba相关库的安装：Mamba环境配置；

安装causal_conv1d和mamba_ssm时尽量使用whl文件：causal_conv1d-1.1.1+cu118torch2.1cxx11abiFALSE-cp310-cp310-linux_x86_64.whl、mamba_ssm-1.1.1+cu118torch2.1cxx11abiFALSE-cp310-cp310-linux_x86_64.whl。

其他内容

论文中提及的其他视觉表示学习模型：CNN系列：VGG、Resnet、EfficientNet；ViT系列：ViT、Swin、DeiT。