本文包含的内容：

• KNN问题，ANN问题，相关算法的分类
• 沃罗诺伊图 (Voronoi Diagram) 和德劳内图 (Delaunay Graph) 的基础知识，以及相关定理的证明
• MSNET (Monotonic Search Network) 的基础知识，以及相关定理的证明
• RNG (Relative Neighborhood Graph) 的基础知识
• MRNG (Monotonic Relative Neighborhood Graph) 的基础知识，以及相关定理的证明
• NSG (Navigating Spreading-out Graph) 的基础知识，以及相关定理的证明

指数加权平均

我们考虑以下场景：你开了一家店，需要根据前几年的收入预测今年收入，也就是序列数据的预测问题。这时候最简单的就是取平均值，但是这样就损失了序列数据的特点，即时间上越靠近现在，其数值对当前的影响越大。此时，我们可以使用指数加权平均：

$$\begin{aligned}&V_0=0\\&V_t=\beta V_{t-1}+(1-\beta)\theta_t\end{aligned}$$

什么是损失函数

一言以蔽之，损失函数（loss function）就是用来度量模型的预测值$f(x)$与真实值$Y$的差异程度的运算函数，它是一个非负实值函数，通常使用$L(Y, f(x))$来表示，损失函数越小，模型的鲁棒性就越好。

评价指标与损失函数的区别？

当建立一个学习算法时，我们希望最大化一个给定的评价指标matric（比如说准确度），但算法在学习过程中会尝试优化一个不同的损失函数loss（比如说MSE/Cross-entropy）。

那为什么不把评价指标matric作为学习算法的损失函数loss呢？

1. 一般来说，应该尝试优化一个与你最关心的评价指标相对应的损失函数。

   例如，在做分类时，我认为你需要给我一个很好的理由，让我不要优化交叉熵。但是，交叉熵并不是一个非常直观的指标，所以一旦你完成了训练，你可能还想知道你的分类准确率有多高，以了解你的模型是否真的能在现实世界中发挥作用。

   总之，在每个epoch训练完后，你都会有多个评估指标。这样作的主要原因是为了了解你的模型在做什么。这意味着你想要最大化指标A，以便得到一个接近最大化指标B的解决方案。

2. 通常情况下，MSE/交叉熵比精度更容易优化，因为它们对模型参数是可微的，在某些情况下甚至是凸的，这使得它更容易。

   在可微的条件下，或许你还想要梯度更容易计算(交叉熵v.s.dice-coefficient或者IoU)。在语义分割的情况下使用交叉熵而不是dice或者类似的IoU指标，这是因为交叉熵的梯度更好。

vscode相关

无代码补全

一般是python编辑器的问题，注意是否激活了python环境。如果也无法激活python环境，就检查一下python的几个扩展是否存在问题，特别是pylance，尤其是其可能未【启用】。

再记录一个很好用的vscode扩展：IntelliCode Completions，IntelliCode Completions根据当前上下文预测一整行代码。预测显示为灰色文本在光标的右侧。此扩展支持Python、JavaScript和TypeScript。

NaN and Inf

参考：CSDN：Pytorch定位NaN

vscode相关

• VSCode将一份代码同步到多台服务器的解决方案：用sftp，在config中设置双设备。

其他内容

• 混合精度训练：
  • 更关注理论层面：知乎：浅谈混合精度训练
  • 更关注代码层面：CSDN：详解混合精度训练（Mixed Precision Training）

CNN的核心功能是特征提取与选择，本质上是一种输入到输出的映射。

池化

池化过程在一般卷积过程后。池化（pooling） 的本质，其实就是采样。Pooling 对于输入的 Feature Map，选择某种方式对其进行降维压缩，以加快运算速度。

池化有两种，最大池化和平均池化。【池化层没有参数、池化层没有参数、池化层没有参数】 （重要的事情说三遍）

池化的作用：

• 保留主要特征的同时减少参数和计算量，防止过拟合。
• invariance(不变性)，这种不变性包括translation(平移)，rotation(旋转)，scale(尺度)。

昇腾大模型|结构组件-1——Layer Norm、RMS Norm、Deep Norm

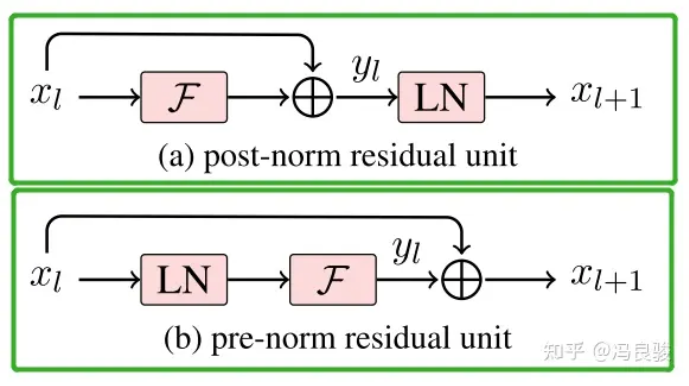
一般认为，Post-Norm在残差之后做归一化，对参数正则化的效果更强，进而模型的收敛性也会更好；而Pre-Norm有一部分参数直接加在了后面，没有对这部分参数进行正则化，可以在反向时防止梯度爆炸或者梯度消失，大模型的训练难度大，因而使用Pre-Norm较多。

Sigmoid

问：为什么大模型会有梯度消失问题？

答：sigmoid函数的导数取值范围是(0, 0.25]，小于1的数乘在一起，必然是越乘越小的。这才仅仅是3层，如果10层的话， 根据$0.25^{10}≈ 0.000000954$，第10层的误差相对第一层卷积的参数的梯度将是一个非常小的值，这就是所谓的“梯度消失”。