跳至主要內容

评价指标总结

Genhiy...大约 7 分钟AI评价指标

评价指标与损失函数的区别？

当建立一个学习算法时，我们希望最大化一个给定的评价指标matric（比如说准确度），但算法在学习过程中会尝试优化一个不同的损失函数loss（比如说MSE/Cross-entropy）。

那为什么不把评价指标matric作为学习算法的损失函数loss呢？

  1. 一般来说，应该尝试优化一个与你最关心的评价指标相对应的损失函数。

    例如，在做分类时，我认为你需要给我一个很好的理由，让我不要优化交叉熵。但是，交叉熵并不是一个非常直观的指标，所以一旦你完成了训练，你可能还想知道你的分类准确率有多高，以了解你的模型是否真的能在现实世界中发挥作用。

    总之，在每个epoch训练完后，你都会有多个评估指标。这样作的主要原因是为了了解你的模型在做什么。这意味着你想要最大化指标A，以便得到一个接近最大化指标B的解决方案。

  2. 通常情况下，MSE/交叉熵比精度更容易优化，因为它们对模型参数是可微的，在某些情况下甚至是凸的，这使得它更容易。

    在可微的条件下，或许你还想要梯度更容易计算(交叉熵v.s.dice-coefficient或者IoU)。在语义分割的情况下使用交叉熵而不是dice或者类似的IoU指标，这是因为交叉熵的梯度更好。

分类问题离线指标

提示

本部分内容部分参考：知乎：F1、ROC、AUC的原理、公式推导、Python实现和应用open in new window

常见分类问题评价指标的问题：

  • 精确率、召回率、F1的局限：二分类时只能评估正类的分类性能，多分类时只能评估某一类的分类性能。
  • 正确率、错误率的难点：对于二分类：正类和负类是相对的，对于多分类：如何选取阈值。

AUC

AUC（Area Under the ROC Curve），ROC曲线下的面积。ROC（Receiver Operating Characteristic）Curve，受试者工作特征曲线：不同分类阈值下的真正类率（TPR）和假正类率（FPR）构成的曲线。

AUC的定义：随机抽出一对样本（一个正样本、一个负样本），然后用训练得到的分类起来对这两个样本进行预测，预测得到的正样本的概率大于负样本的概率的概率。AUC考虑的是样本预测的排序质量。

AUC(R)n=1∣R∣(n−∣R∣)∑r∈R∑r′∈({1,…,n}∖R)δ(r<r′)=n−∣R∣−12−1∣R∣∑r∈Rrn−∣R∣ \begin{gathered} \mathrm{AUC}(R)_{n} =\frac{1}{|R|(n-|R|)}\sum_{r\in R}\sum_{r^{\prime}\in(\{1,\ldots,n\}\setminus R)}\delta\left(r<r^{\prime}\right) \\ =\frac{n-\frac{|R|-1}2-\frac1{|R|}\sum_{r\in R}r}{n-|R|} \end{gathered}

AUC的计算方法：

AUC为正样本得分大于负样本得分的概率，但是穷举正负样本对太复杂，可以先根据得分从小到大排序，然后找出每个正样本的排序位次。计算出每个位次下负样本的个数，就是该正样本得分大于负样本得分的次数，对次数进行累加就是所有正样本得分大于负样本得分的次数，除以M×NM×N就是所有正样本得分大于负样本得分的概率，如下图所示：

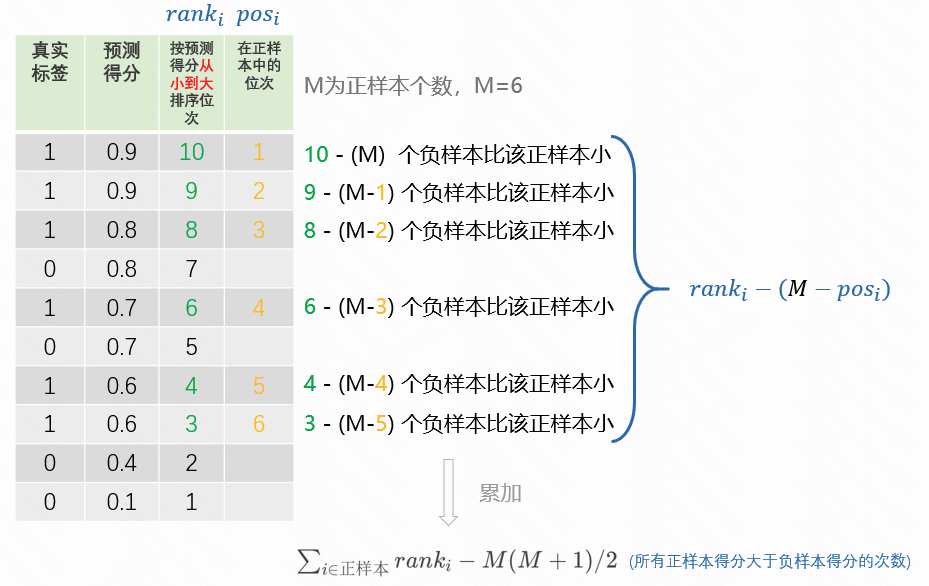
所以最终AUC的公式为：

AUC=∑i∈ 正样本 rank⁡i−M(M+1)/2M×N AUC=\frac{\sum_{i \in \text { 正样本 }} \operatorname{rank}_{i}-M(M+1) / 2}{M \times N}

AUC有两个明显优势：一是体现相对的排序（例如0.9排在0.1前面和0.5排在0.1前面对他来说是一样的）；二是适用样本不均衡情况。

AUC也有三个劣势：

  • 无法反应Top-N的效果；AUC反映的是相对有序效果，但不能反映Top-N的效果，实际上我们更关注头部，比如推荐、搜索、广告方面。
  • 只反映了排序能力，关注的是概率值的相对大小，与阈值和概率值的绝对大小没有关系，没有反映预测精度；（简单说，如果对一个模型的点击率统一乘以2，AUC不会变化，但显然模型预测的值和真实值之间的offset扩大了。）
  • AUC只关注正负样本之间的排序，并不关心正样本内部，或者负样本内部的排序。这也体现了AUC的本质：任意个正样本的概率都大于负样本的概率的能力。

门捷列夫说“没有测量，就没有科学”。

精确率、召回率、 F1、ROC、AUC就是机器学习中基础且应用广泛的测量评估方法。但它们都是一些常用的离线指标 ，像推荐系统、计算广告等这些跟业务紧密联系的业务，还需要线上评估指标，这时就要考虑A/B实验：

A/B实验

提示

本部分内容部分参考：知乎：A/B测试(AB实验)的基础、原理、公式推导、Python实现和应用open in new window

基本信息

首先，什么是A/B测试？A/B测试是一种随机测试（试验），将两个不同的东西（A、B）进行假设比较。A/B测试也称对照试验（Controlled Experiments）、双盲试验（Double Blind Clinical Trial）。

  • A/B测试的核心步骤：假设、检验。
  • A/B测试的流程：假设、抽样、检验、结论。
  • A/B测试的统计学基础：试验设计、抽样理论、假设检验。

常见的A/B测试工具，它们的输入，输出都是什么？

  • powerandsamplesize 输入是：样本量（Sample Size）、统计功效（Power）、显著性水平 （Type Ι error rate）。
  • 字节跳动的 DataTester 输出是：置信区间（confidence interval）、p值（p-value）、检验灵敏度（MDE）。

统计学基础

  • 大样本与小样本：大样本、小样本之间并不是以样本量大小来区分的，只要样本量固定条件下进行的统计推断、问题分析，不管样本量多大，都称为小样本问题。

  • Z分布：标准正态分布，又称为U分布，无论样本数据怎么变化，Z分布始终不变。

  • t分布：当N很大时，t分布类似于Z分布，一般来说，n=30时即近似等价于标准正态分布。

  • 卡方分布：服从N(0,1)N(0,1)分布的样本的平方和所服从的分布。

  • 中心极限定理：习惯于把和的分布收敛于正态分布的那一类定理都叫做“中心极限定理”。

  • 原假设与备择假设：原假设指实验之前原有的假设，备择假设指如果否定原假设，可备选择的假设。A/B实验中，原假设指AB组指标无显著差异，备择假设指AB组有显著差异。

  • 第一、二类错误：第一类错误指实际上新策略无效，但实验显示有效；第二类错误指实际上新策略有效，但实验显示新策略无效。

  • 显著性水平：显著性水平（significance level），使得犯第 Ι 类错误的概率控制在一给定的水平下，这个水平就是显著性水平，在此基础上使犯第 ΙΙ 类错误的概率尽可能小。

  • p值：

    • 定义1：p 值（probability value，p -value）在观测数据下拒绝原假设的最小显著性水平。
    • 定义2：p 值是指拒绝原假设犯第 Ι 类错误的最小概率。
    • 定义3：p 值代表观察到的随机因素产生的差异概率。

  • 统计功效（statistical power）：不犯第ΙΙ类错误（1-β）的概率。A/B实验中的统计功效：当AB两组差异真的存在时，能正确判断的概率。统计功效的影响因素：两总体差异（效应量）、显著性水平 α、样本量 n。但是，在这 3 个影响因素中，显著性水平 α 是提前给定，只有样本量 n 是可以控制的。

  • 效应量（Effect Size，又称效应值），提供了对效应大小的具体测量。效应量的特征：不依赖样本量，不依赖测量尺度，效应量的正负号仅表示效应的方向，其绝对值才是实际的效应大小。

  • 其他内容：置信区间、置信度。

重要

P值、置信区间、效应量是衡量试验结果的三个最重要的指标。

努力把生活过成诗
Copyright © 2024 Genhiy